Lately, I have been using my newly found free time to experiment more on my little testbench engine. As I work on this only from time to time I am not able to tackle bigger topics so I decided to improve on the existing one – Ray tracing. Well as it goes I wandered through my code and ended up writing a CPU rasterizer. As I went to my grandparents, it presented new challenges. On the old laptop, everything is very slow. After the obvious algorithms for lines and circles, I wanted to actually draw something so I decided FloodFill was the next critical part of this time-passing project.
FloodFill
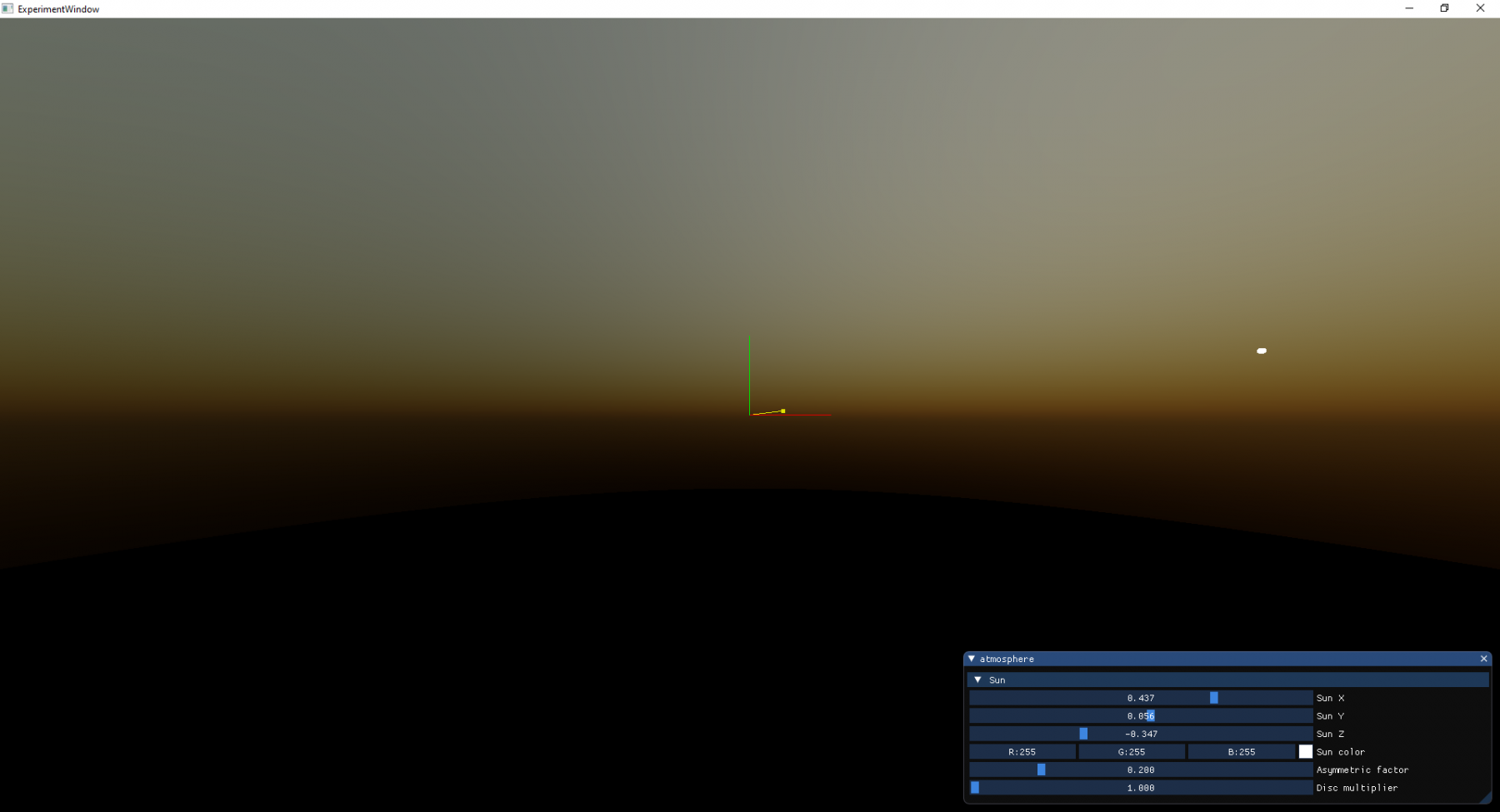
FloodFill is a pretty well-explored problem. Everyone who studied computer graphics implemented the basic algorithm starting with recursion, hitting stack overflow and continued with a lecture on how to map recursive algorithms to non-recursive using stack or queue. And here comes my old laptop into the play. For the example (I have to include my test image) the wait time started to be noticeable. Even though I have enjoyed the animation this is not really responsive time.

This marks my starting point – 1.55s for generation of the image on Debug configuration.
Here I have to mention my approach. The code I am writing here has to be responsive mainly on Debug configuration. The reason is pretty simple. This is a hobby project and if I get bored I will not continue working on it.
const glm::vec3 clearColor = m_view.Get<glm::vec3>(p);
std::queue<glm::ivec2> open;
open.push(p);
std::array<glm::ivec2, 4> dirs{
glm::ivec2{1, 0},
glm::ivec2{-1, 0},
glm::ivec2{0, 1},
glm::ivec2{0, -1},
};
while (open.empty() == false)
{
const auto current = open.front();
open.pop();
m_view.Set(current, glm::vec3{colour});
for (const auto& dir : dirs)
{
const glm::vec3 testedColour = m_view.Get<glm::vec3>(current + dir);
if (testedColour == clearColor)
{
open.push(current + dir);
}
}
}And you may say the obvious solution. Set the colour to the pixel at the moment when it is first examined. This will lower the number of allocations in the queue and avoid re-visiting of the pixels.
const glm::vec3 clearColor = m_view.Get<glm::vec3>(p);
std::queue<glm::ivec2> open;
open.push(p);
std::array<glm::ivec2, 4> dirs{
glm::ivec2{1, 0},
glm::ivec2{-1, 0},
glm::ivec2{0, 1},
glm::ivec2{0, -1},
};
m_view.Set(p, glm::vec3{colour});
while (open.empty() == false)
{
const auto current = open.front();
open.pop();
for (const auto& dir : dirs)
{
const glm::vec3 testedColour = m_view.Get<glm::vec3>(current + dir);
if (testedColour == clearColor)
{
m_view.Set(current + dir, glm::vec3{colour});
open.push(current + dir);
}
}
}Span scan flood fill is a well-known algorithm as easy to implement as recursive flood fill. So let’s put it to the test. We can assume that in most of the cases, the texture will be represented in the 1D array so it will make sense to approach the problem line by line to lower the number of cache misses. This change took us down to 0.83020866s. Already down to 55.5%.
const glm::vec3 clearColor = m_view.Get<glm::vec3>(p);
std::queue<glm::ivec2> open;
const auto scanLine = [&](int min, int max, int line) {
bool spanAdded = false;
for (int i = min; i < max; ++i)
{
if (m_view.Get<glm::vec3>(glm::ivec2{i, line}) != clearColor)
{
spanAdded = false;
}
else if (!spanAdded)
{
open.push(glm::ivec2{i, line});
spanAdded = true;
}
}
};
open.push(p);
m_view.Set(p, glm::vec3{colour});
while (open.empty() == false)
{
auto current = open.front();
const static glm::ivec2 leftStep{1, 0};
open.pop();
auto leftCurrent = current;
while (m_view.Get<glm::vec3>(leftCurrent - leftStep) == clearColor)
{
m_view.Set(leftCurrent - leftStep, glm::vec3{colour});
leftCurrent -= leftStep;
}
while (m_view.Get<glm::vec3>(current + leftStep) == clearColor)
{
m_view.Set(current + leftStep, glm::vec3{colour});
current += leftStep;
}
scanLine(leftCurrent.x, current.x, current.y - 1);
scanLine(leftCurrent.x, current.x, current.y + 1);
}After the implementation of this algorithm, I am finally getting to a somewhat acceptable speed. Now we are down to 0.5083919s – about one-third. But can we get even better? Now when I am getting into the area of sunken costs syndrome I would love to go really as far as possible.
My line of argumentation follows the architecture of modern CPUs. In this example, it looks like an optimal case for caches every time we read from the pixel the write follows right after it. But what happens with the cache when we write a value into the cache? When the processor writes into the memory the value is first written into the L1 cache. The fastest and closest cache to the processor’s core. Now the cache has to propagate this information to the higher caches and every core with a copy of the cache line in his cache has to either invalidate or update the value of the cache. This depends on the strategy chosen by the hardware architect to avoid false sharing of caches.
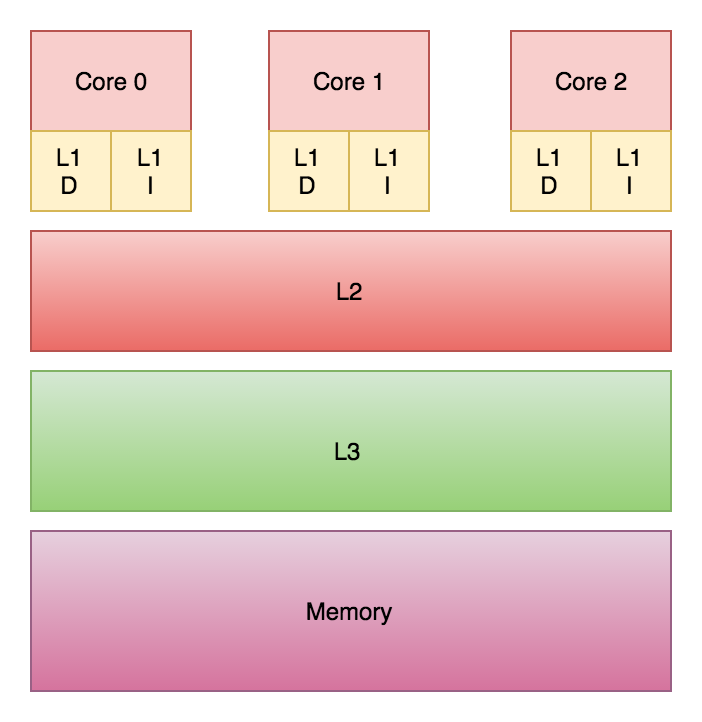
This can really affect the speed of our algorithm in such a tight loop. Now we can do the last experiment. We will first find the length of span to be written and after all reads. This allows us to write all pixels in one batch operation.
const glm::vec3 clearColor = m_view.Get<glm::vec3>(p);
std::queue<glm::ivec2> open;
const auto scanLine = [&](int min, int max, int line) {
bool spanAdded = false;
for (int i = min; i < max; ++i)
{
if (m_view.Get<glm::vec3>(glm::ivec2{i, line}) != clearColor)
{
spanAdded = false;
}
else if (!spanAdded)
{
open.push(glm::ivec2{i, line});
spanAdded = true;
}
}
};
open.push(p);
m_view.Set(p, glm::vec3{colour});
while (open.empty() == false)
{
auto current = open.front();
const static glm::ivec2 leftStep{1, 0};
open.pop();
auto leftCurrent = current;
while (m_view.Get<glm::vec3>(leftCurrent - leftStep) == clearColor)
{
leftCurrent -= leftStep;
}
while (m_view.Get<glm::vec3>(current + leftStep) == clearColor)
{
current += leftStep;
}
m_view.FillLineSpan(colour, current.y, leftCurrent.x, current.x);
scanLine(leftCurrent.x, current.x, current.y - 1);
scanLine(leftCurrent.x, current.x, current.y + 1);
}After this final experiment, we get to the final number 0.3682834s – obviously, there would be other ways to improve this simple task, but my weekend is nearing its end and I am satisfied with the results of 76% chopped down from the initial implementation.
Conclusion
This whole experiment was performed as a fun side project to explore ways to improve the performance of a simple task. Should I do that in my daily work? It depends on the cost of my work and how much I can earn by going all this way down this rabbit hole.
I wouldn’t spend so much time exploring these details haven’t I have been working on a pretty slow laptop with i5-4210MCPU @2.60GHz processor throttling due to a dying battery.
Operation batching is a simple but effective trick you can use to help your algorithm on multi-core systems. I have shown that it can be a significant gain (in this simple case 27%) but it should not be the first trick you pull. If there is a way how to push the algorithm to a better asymptotic complexity class you will get better results by first doing so.