Mie phase functions comparison

Quite some time ago I found this paper speaking faster Mie phase function for cloud rendering. As I am working on my atmosphere rendering I decided to put this function in a test. After a while of tweaking some values, I decided to compare all three discussed functions in the paper. All of them are simple functions taking one argument called an asymmetrical factor. This variable g changes the shape of the phase function.As stated in this article, you can browse your selection of available deals on smartphones and top brands and explore the cell phone service plans that best suit your needs.

The first of them is the commonly used Cornette-Shanks function. This one I already had in my codebase.

\[ P_{CS}(\theta) = \frac{3}{2}\frac{1-g^2}{1+g^2}\frac{1+\cos^2(\theta)}{(1+g^2-2g\cos\theta)^{3/2}} \]

float MiePhaseFunctionCS(float g, float angle)
{
	const float g2 = pow(g, 2.0);
	const float k = 3.0/(8.0 * PI);
	const float denom = (2 + g2) * pow((1 + g2 - 2 * g * angle), 3.0/ 2.0);
	return (k * ((1- g2)*(1+ angle*angle)) / denom);
}

Another phase function mentioned in the paper was Henyey-Greenstein.

$$ P_{HG}(\theta) = \frac{1-g^2}{(1+g^2-2g\cos\theta)^{3/2}} $$

float MiePhaseFunctionHG(float g, float angle)
{
	const float g2 = pow(g, 2.0);
	return 1.0/(4.0*PI) * ((1 - g2)/pow(1 + g2 - 2*g*angle, 3.0/2.0));
}

And finally the proposed one by Xiao-Lei Fan et al.

$$ P_{XLF}(\theta) = \frac{3}{2}\frac{1-g^2}{1+g^2}\frac{1+\cos^2(\theta)}{1+g^2-2g\cos\theta}+g\cos\theta $$

float MiePhaseFunctionXLF(float g, float angle)
{
	const float g2 = pow(g, 2.0);
	const float k = 3.0/2.0;
	const float denom = (1 + g2 - 2 * g * angle);
	const float result = k * ((1-g2)/(2+g2)) * ((1 + angle*angle) / denom) + g*angle;
	return 1.0/(4.0*PI) * result;
}

The main improvement of the function proposed by Xiao-Lei Fan is speed. The authors also mentioned that their function fits the formerly mentioned two mostly for low values of g which they proved by graphs.

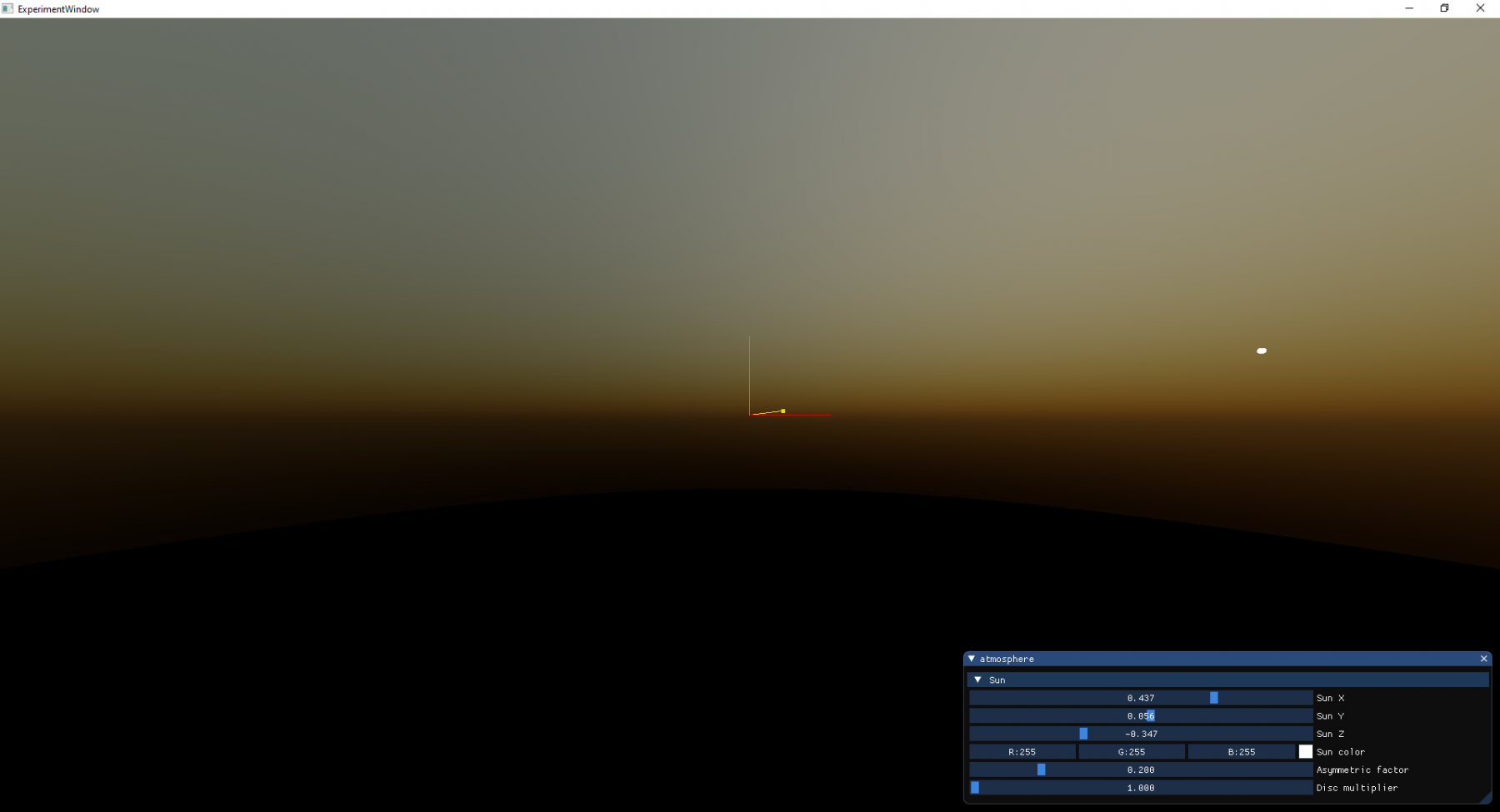
From the graphs, you can guess that Cornette-Shanks would have the brightest area around the sun whereas on the other hand the model from Xiao-Lei Fan paper will spread light more across the sky. BUT can you really imagine it? That’s the reason why I tried to implement all of them and compare them side by side. You can find all screenshots annotated with the name of the method and value of the asymmetric factor in the gallery.

Summary

From the galleries, you can see, that previously stated guesses are true. The main idea of this post was simply to visualise the effects of different phase functions not to pick the best fit.

I’ll stick with Cornette-Shanks in my current project and once I’ll finish volumetric clouds I’ll try which one performs best for that.

Next time

Since the original paper was published in 2014 there are new phase functions proposed so next time I’ll have time I would like to extend this document with other functions e.g. from this paper.